Gegeben:
Gesucht:
M1 (x1, y1) Koordinaten des Mittelpunktes von Kreis k1 R1 Radius des Kreises k1 M2 (x2, y2) Koordinaten des Mittelpunktes von Kreis k2 R2 Radius des Kreises k2
Man berechnet erst den Abstand der Mittelpunkte d zueinander. Dann führt man eine Fallunterscheidung durch.
Relative Lage der Kreise zueinander
Gesucht:
M1 (x1, y1) Koordinaten des Mittelpunktes von Kreis k1 R1 Radius des Kreises k1 M2 (x2, y2) Koordinaten des Mittelpunktes von Kreis k2 R2 Radius des Kreises k2
Es wird vorausgesetzt, dass ein Kreis vollkommen innerhalb des anderen liegt. Für die Berechnung von Eilinien muss der Abstand d der Kreislinien berechnet werden. Zu dessen Berechnung sind folgende Werte ausschlaggebend:
d Abstand der Kreislinien
Es wird nun angenommen, dass R2 größer oder gleich R1 ist. Ist das nicht der Fall, so vertauscht man die Kreise, um die Annahme sicher zu stellen.
- Radius R1 des Kreises 1
- Radius R2 des Kreises 2
- Abstand der Punkte M1 M2
d = |R2| - a - |R1|
Gesucht:
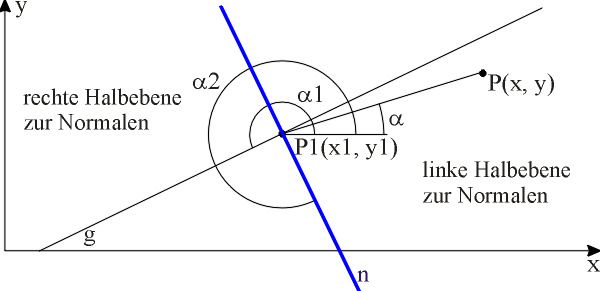
P1 (x1, y1) Koordinaten eines Punktes auf der Bahnstrecke a1 Richtungswinkel des Gleises in diesem Punkt P (x, y) Koordinaten des zu betrachtenden Punktes P
Es wird wie immer nur die x-y-Ebene betrachtet.
relative Lage des Punktes P zur Strecke
| Ist der Abstand P1-P = 0, so liegt der Punkt auf der Geraden, die Berechnung ist beendet | ||||||||
| Berechne den Winkel a, dieser ist der Richtungswinkel der Geraden durch P1 und P | ||||||||
|
Gesucht:
P1 (x1, y1) Punkt auf der Geraden g a1 Richtungswinkel der Geraden g P (x, y) Koordinaten des zu betrachtenden Punktes P
Der Algorithmus zur Berechnung des Abstandes ergibt sich aus den Formeln zu Geradengleichung in Normalform und dem Abstand des Punktes von einer Geraden§5.
d Abstand des Punktes P von g
x * cosa + y * sina - p = 0Man stellt diese Gleichung nach p um und setzt für x und y die Koordinaten von P1, für a a1 + p ein.
d = | x * cosa + y * sina - p |Dabei sind x und y die Koordinaten von P.
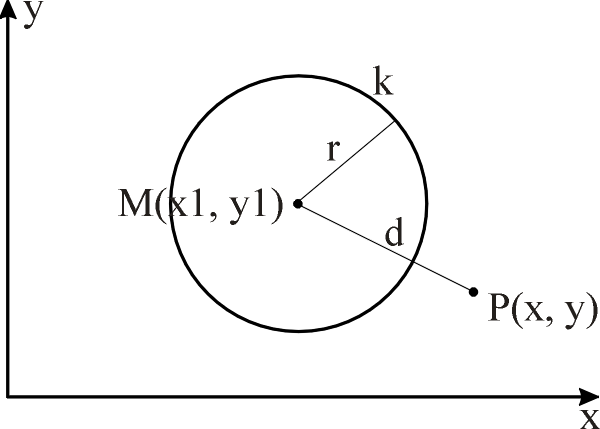
Gesucht:
M (x1, y1) Koordinaten eines Kreismittelpunktes r Radius des Kreises P (x, y) Koordinaten des zu betrachtenden Punktes P
Man unterscheidet bei der relativen Lage eines Punktes zu einem Kreis drei Fälle:
Relative Lage des Punktes P zum Kreis
Gesucht:
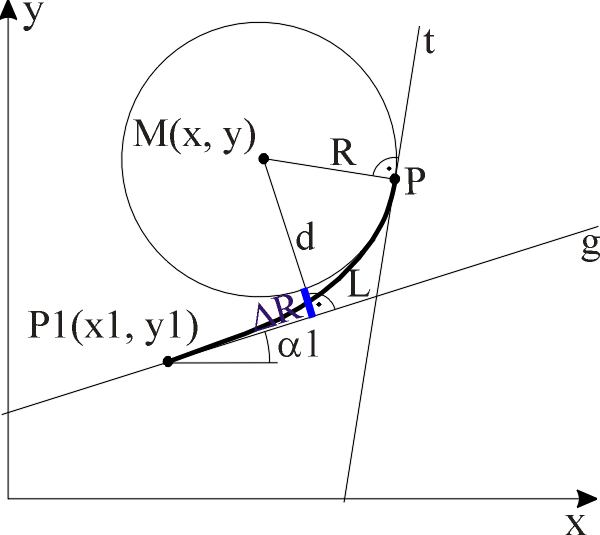
M (x, y) Mittelpunkt des Kreises k R Radius des Kreises P1 (x1, y1) Punkt auf der Geraden g a1 Richtungswinkel der Geraden g
Zur Berechnung der Klotoide von g nach k muss die Tangentenabrückung DR berechnet werden. Diese ergibt sich wie folgt:
DR Tangentenabrückung des Kreises
DR = d - |R|d ist dabei der Abstand von M zu g
Gesucht:
kl Geometrie-Element Klotoide L Zurückgelegte Länge auf der Klotoide
Ist nur die Klotoide gegeben, so berechnet man erst die Gleichung der Geraden g sowie den Kreismittelpunkt M. Mit diesen Daten lässt sich obiges Schema anwenden.
DR Tangentenabrückung des Kreises
a1 + L / (2R)Mit dem Richtungswinkel von t und R erhält man die Koordinaten von M.