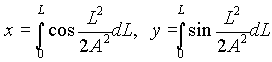![[previous]](left.gif)
![[map]](map.gif)
![[next]](right.gif)
2.1 Geometrie-Elemente
Um den Verlauf einer Straße oder eines Gleises zu beschreiben verwendet
man Geometrie-Elemente. Die Trassierung einer Strecke erfolgt dabei durch
eine Kette verschiedener Geometrie-Elemente. Im Laufe
der Zeit haben sich die Geometrie-Elemente Gerade, Kreis und Klotoide
als Standard bei der Trassierung etabliert.
2.1.1 Gerade
Die Gerade ist das einfachste Geometrie-Element. Streng genommen handelt
es sich bei diesem Element nicht um eine Gerade, sondern um eine Strecke.
Zur eindeutigen Beschreibung einer Strecke in der x- y-Ebene benötigt
man vier Parameter. Man kann zum Beispiel die x- und y-Koordinaten des
Start- und Endpunktes verwenden. Statt sich die Koordinaten des Endpunktes
zu merken, bietet es sich an, die Richtung und die Länge der Strecke
zu speichern. Verwendet man nun für die x- y-Koordinaten und Richtung
jeweils die Endwerte des vorhergehenden Geometrie-Elements, so reicht es,
sich bei einer Strecke dessen Länge l zu speichern.
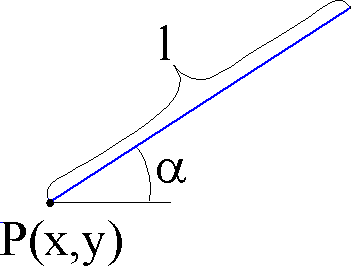
Beschreibende Parameter:
-
x-Koordinate des Startpunktes P
-
y-Koordinate des Startpunktes P
-
Richtungswinkel a
-
Länge der Strecke l
2.1.2 Kreis
Zur Modellierung von Kurven wird das Trassierungselement Kreis verwendet,
analog zur Gerade handelt es sich dabei nicht um einen Vollkreis, sondern
nur um einen Ausschnitt. Zur eindeutigen Darstellung des Elementes Kreis
in der x- y-Ebene benötigt man fünf Werte. Man verwendet dazu:
x- und y-Koordinaten des Startpunktes, den Richtungswinkel, die Krümmung
und die Länge des Kreissegmentes. Anhand des Vorzeichens der Krümmung
wird unterschieden, ob man den Kreis im Uhrzeigersinn (negatives Vorzeichen)
oder dagegen durchläuft (positives Vorzeichen). So gesehen wäre
eine Gerade ein Sonderfall des Kreises, bei dem die Krümmung null
ist. Der Radius des Kreises ergibt sich
aus dem Kehrwert der Krümmung. Er kann damit auch negative Werte annehmen.
Nimmt man nun für die x- und y-Koordinaten sowie die Richtung die
Endwerte des vorhergehenden Geometrie-Elementes, so müssen nur noch
die Länge und der Radius des Kreises verwaltet werden. Auf letzteren
könnte man streng genommen auch verzichten, wenn man dafür den
Radius am Ende des letzten Geometrie-Elementes verwendet.
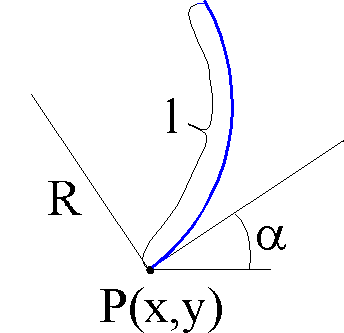
Beschreibende Parameter:
-
x-Koordinate des Startpunktes P
-
y-Koordinate des Startpunktes P
-
Richtungswinkel a
-
Krümmung 1/R
-
Länge des Segmentes l
2.1.3 Klotoide
2.1.3.1 Definition
Verwendet man zur Beschreibung einer Trasse nur die Geometrie-Elemente
Kreis und Gerade so kommt es an den Übergangspunkten zu einer sprunghaften
Änderung der Krümmung. Nach dem zweiten Newtonschen Gesetz gilt
die Formel F = a * m bzw. F = (m * v2 ) / r. Der Radius r ist
der Kehrwert der Krümmung. Überfährt man nun mit einem Schienenfahrzeug
die Stelle, an der der Krümmungssprung auftritt, so führt dies
zu einer ruckartig ansteigenden Beschleunigung. Auch im Straßenverkehr
sollten solche Krümmungssprünge vermieden werden. Da das Fahrzeug
nicht geführt wird, tritt hier zwar keine ruckartige Beschleunigung
auf, jedoch wird der Fahrer intuitiv dazu gezwungen, langsamer zu fahren
oder die Gegenfahrbahn zu schneiden. Er ist nämlich nicht in der Lage,
den Einschlag des Lenkrades in einem unendlich kurzen Zeitraum von einer
Lage in eine andere zu ändern, was notwendig wäre, um den Krümmungssprung
nachvollziehen zu können.
 Als erste Lösung bietet es sich an, zwischen Gerade und Endradius
einen zweiten Kreisbogen mit größerem Radius zu schalten. Dadurch
kompensiert man den großen Krümmungssprung, der bei direktem
Übergang in den Endradius auftreten würde, durch zwei Krümmungssprünge,
die nur halb so groß sind. Dies schafft für den Anfang Abhilfe.
Diese Methode eignet sich jedoch nur bedingt, um die fahrpsychologischen
Ansprüche zu erfüllen. In den meisten Fällen wird nach wie
vor eine ruckartige Beschleunigung spürbar sein, bzw. das Durchfahren
der Kurve wird als unbehaglich empfunden werden.
Als erste Lösung bietet es sich an, zwischen Gerade und Endradius
einen zweiten Kreisbogen mit größerem Radius zu schalten. Dadurch
kompensiert man den großen Krümmungssprung, der bei direktem
Übergang in den Endradius auftreten würde, durch zwei Krümmungssprünge,
die nur halb so groß sind. Dies schafft für den Anfang Abhilfe.
Diese Methode eignet sich jedoch nur bedingt, um die fahrpsychologischen
Ansprüche zu erfüllen. In den meisten Fällen wird nach wie
vor eine ruckartige Beschleunigung spürbar sein, bzw. das Durchfahren
der Kurve wird als unbehaglich empfunden werden.
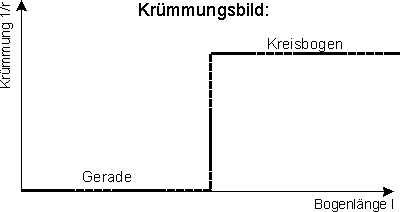
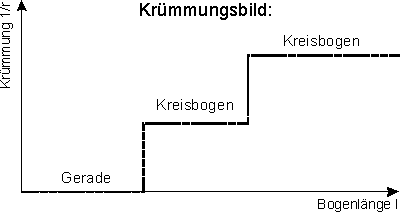 Im nächsten Schritt könnte man dazu übergehen, die zwei
Krümmungssprünge wieder zu halbieren, in dem man weitere Zwischenradien
einführt. Setzt man diese Methode fort, so erhält man als Krümmungsbild
eine Art Treppe, die mit jedem Iterationsschritt immer kleinere Stufen
und damit Krümmungssprünge aufweist. Man könnte jetzt so
oft iterieren, bis die Krümmungssprünge so klein werden, daß
diese beim Durchfahren der Trasse nicht mehr wahrgenommen werden. Dies
ist bei Radiussprüngen < 10 % der Fall §2.
Man kann aber auch unendlich oft iterieren, was dazu führt, dass jedem
Punkt der Strecke ein anderer Radius zugeordnet wird. Es tritt kein Krümmungssprung
mehr auf da sich die Krümmung nun linear ändert. Die Krümmung
ist bei der Klotoide proportional zur Länge vom Startpunkt.
Im nächsten Schritt könnte man dazu übergehen, die zwei
Krümmungssprünge wieder zu halbieren, in dem man weitere Zwischenradien
einführt. Setzt man diese Methode fort, so erhält man als Krümmungsbild
eine Art Treppe, die mit jedem Iterationsschritt immer kleinere Stufen
und damit Krümmungssprünge aufweist. Man könnte jetzt so
oft iterieren, bis die Krümmungssprünge so klein werden, daß
diese beim Durchfahren der Trasse nicht mehr wahrgenommen werden. Dies
ist bei Radiussprüngen < 10 % der Fall §2.
Man kann aber auch unendlich oft iterieren, was dazu führt, dass jedem
Punkt der Strecke ein anderer Radius zugeordnet wird. Es tritt kein Krümmungssprung
mehr auf da sich die Krümmung nun linear ändert. Die Krümmung
ist bei der Klotoide proportional zur Länge vom Startpunkt.
 Dieses Verfahren führt auf die charakteristische Gleichung der Klotoide.
Sie lautet:
Dieses Verfahren führt auf die charakteristische Gleichung der Klotoide.
Sie lautet:
Hierbei ist:
L die Länge der Klotoide vom Ursprung,
R der Radius an der dazugehörigen Stelle.
A bezeichnet man als Parameter oder charakteristische Größe
der Klotoide.
Für die Einheitsklotoide verwendet man Kleinbuchstaben.
Überträgt man die Werte in ein Koordinatensystem, so erhält
man eine Spirale, die durch den Ursprung O verläuft und sich
asymptotisch um die Punkte 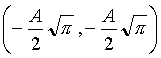 und
und 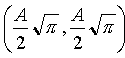 wickelt.
Im Ursprung hat die Klotoide die Krümmung 0, sie ist dort gerade und
verläuft entlang der x-Achse.
wickelt.
Im Ursprung hat die Klotoide die Krümmung 0, sie ist dort gerade und
verläuft entlang der x-Achse.
Für A = 1 ergibt sich die sogenannte Einheitsklotoide:
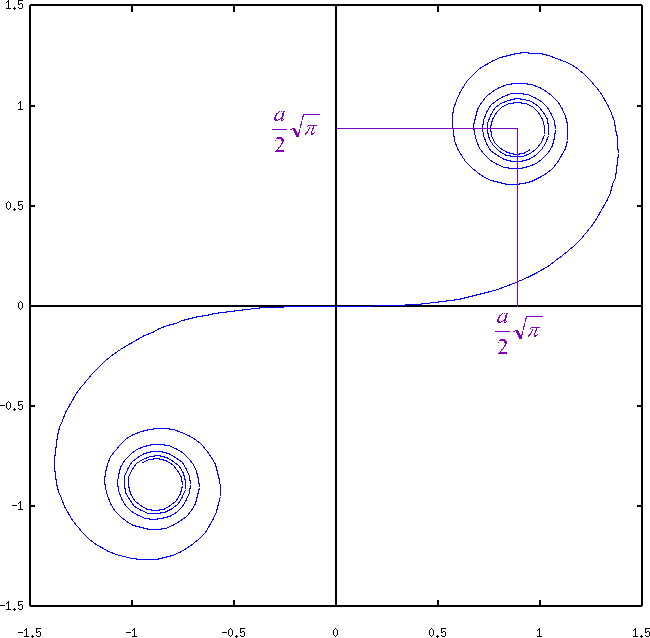 Mit zunehmender Länge reduziert sich dabei der Radius bzw. wächst
die Krümmung.
Mit zunehmender Länge reduziert sich dabei der Radius bzw. wächst
die Krümmung.
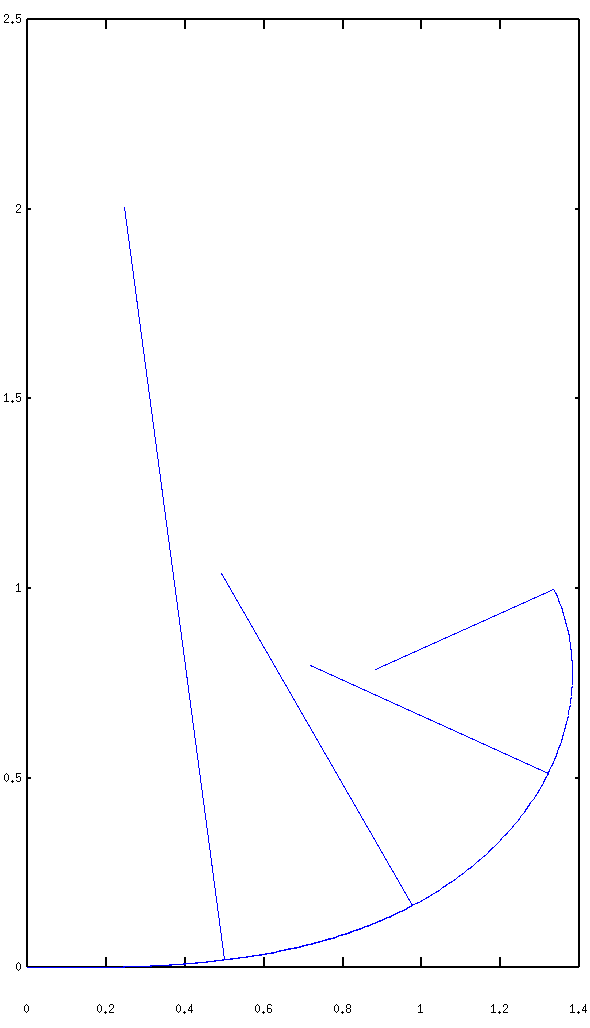 Obiges Schaubild zeigt die Einheitsklotoide von der Länge 0.0 bis
2.0 mit abgetragenen Radien bei den Längen 0.5, 1.0, 1.5, 2.0
Obiges Schaubild zeigt die Einheitsklotoide von der Länge 0.0 bis
2.0 mit abgetragenen Radien bei den Längen 0.5, 1.0, 1.5, 2.0
Das Geometrie-Element Klotoide:
Zur Trassierung verwendet man nur Teilstücke von Klotoiden. Man
benötigt zur eindeutigen Bestimmung des Geometrie-Elementes folgende
Werte:
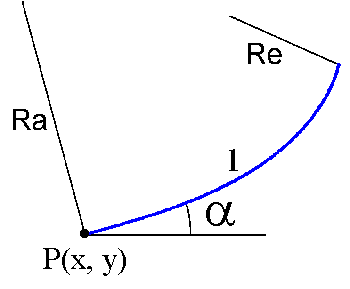 Beschreibende Parameter des Geometrie-Elementes Klotoide:
Beschreibende Parameter des Geometrie-Elementes Klotoide:
-
x-Koordinate des Startpunktes P
-
y-Koordinate des Startpunktes P
-
Richtungswinkel a im Startpunkt P
-
Krümmung 1/Ra im Startpunkt P
-
Länge l der Klotoide
-
Krümmung 1/Re im Endpunkt
Alle Klotoiden sind einander ähnlich§3.
Diese Tatsache machte man sich früher zunutze, indem man die Einheitsklotoide
tabellierte und dann die benötigten Werte nur noch geeignet skalierte.
Es genügte also den Parameter A zu bestimmen und dann sämtliche
Maßzahlen damit zu multiplizieren. Die Winkel bleiben bei der Skalierung
erhalten. Heute ist diese Vorgehensweise nicht mehr nötig, da mit
Hilfe von Programmen die Werte für beliebige Klotoiden direkt genähert
werden können.
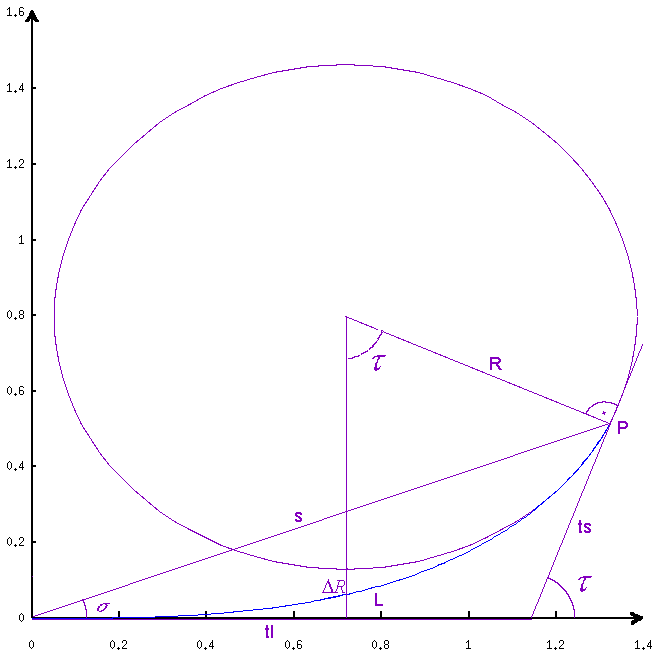 Bei der Berechnung von Trassen sind folgende Klotoidenwerte markant und
werden als gegeben vorausgesetzt oder sind zu berechnen:
Bei der Berechnung von Trassen sind folgende Klotoidenwerte markant und
werden als gegeben vorausgesetzt oder sind zu berechnen:
| s |
Sekantenwinkel |
| t |
Tangentenwinkel |
| L |
Länge der Klotoide von O nach P |
| P |
Ein Punkt auf der Klotoide |
| R |
Radius der Klotoide am Punkt P |
| S |
Länge der Klotoidensehne = Länge der Strecke OP |
| tl |
Länge der langen Tangente |
| ts |
Länge der kurzen Tangente |
| DR |
Tangentenabrückung |
Unter der Tangentenabrückung im Punkt P versteht man den
Abstand des Kreises mit dem Radius R von der x-Achse. R ist
dabei der Radius den die Klotoide im Punkt P besitzt.
2.1.3.2 Wichtige Formeln
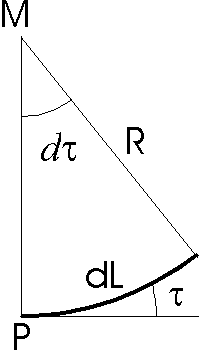
Es gilt:§4
dL = R * dt
Stellt man nun L * R = A2 nach R um und setzt
diese Formel in obige ein, so erhält man:
dL = (A2/L) * dt
bzw.
L * dL = A2 * dt
Integriert man nun diese Gleichung von L = 0 bis L = L erhält
man die Formel
Verknüpft man diese Formel mit der Klotoidengleichung, lassen sich
folgende Zusammenhänge herleiten:
| A2 = L * R = L2 / (2t)
= 2R2t |
t = L / (2R) = L2 /
(2 A2) = A2 / (2R2) |
R = A2 / L = L / (2t) = A
/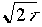 |
L = A2 / R = 2Rt = A
* 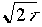 |
2.1.3.3 Berechnung einer Klotoide
Die x- und y-Werte eines Klotoidenpunktes ergeben sich folgendermaßen:
Aus obiger Zeichnung ist ersichtlich:
dx = dL * cost , dy = dL
* sint
mit t = L2/(2A2) erhält
man folgende Gleichungen:
dx = cos(L2/(2A2)) * dL, dy
= sin(L2/(2A2)) * dL
Integriert man nun von 0 bis L, so ergeben sich die Formeln
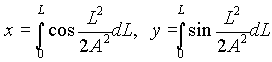
Es handelt sich hierbei um sogenannte FRESNELsche Integrale. Diese
sind nicht geschlossen lösbar. Eine Lösung kann über eine
Reihenentwicklung der Sinus und Cosinusfunktion vorgenommen werden. Die
Summanden sind dann zu integrieren.
Eine genaue Herleitung der Summe sowie eine Fehlerabschätzung
findet man in "Die Klotoide
Formeln Tafeln und Beispiele" ab Formel 9. Somit ist es möglich
die kartesischen Koordinaten eines Punktes zu einer bestimmten Länge
der Klotoide zu berechnen.
![[previous]](left.gif)
![[map]](map.gif)
![[next]](right.gif)



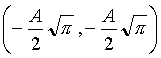 und
und 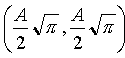 wickelt.
Im Ursprung hat die Klotoide die Krümmung 0, sie ist dort gerade und
verläuft entlang der x-Achse.
wickelt.
Im Ursprung hat die Klotoide die Krümmung 0, sie ist dort gerade und
verläuft entlang der x-Achse.